
Já precisou lidar com muitos números em um projeto e sentiu que as ferramentas comuns não davam conta? Pois é, quem trabalha com dados sabe que, às vezes, precisamos de algo mais eficiente. É aí que entra o NumPy. Essa biblioteca é praticamente uma mão na roda para quem precisa fazer cálculos numéricos em Python, desde operações básicas até matrizes gigantescas.
E o melhor? Ela não só acelera o processo, mas também deixa tudo mais organizado. Se você ainda não conhece ou quer entender melhor como o NumPy pode facilitar sua vida, vem comigo que eu te explico!
O que é o NumPy?
O NumPy (abreviação de Numerical Python) é uma biblioteca de código aberto essencial para a programação em Python quando se trata de computação científica e manipulação de dados numéricos. Criado em 2005 por Travis Oliphant, ele surgiu com o objetivo de unificar duas bibliotecas anteriores, Numeric e Numarray, oferecendo uma solução mais robusta e eficiente para lidar com operações matemáticas complexas. Desde então, tornou-se uma das ferramentas mais utilizadas em áreas como ciência de dados, machine learning e análise científica.
A principal força do NumPy está em seus arrays multidimensionais. Diferentemente das listas comuns do Python, os arrays do NumPy são mais rápidos, ocupam menos memória e permitem realizar operações matemáticas de forma otimizada. Isso se deve ao conceito de vetorização, que permite aplicar operações diretamente sobre grandes conjuntos de dados sem precisar recorrer a loops.
Além de cálculos matemáticos básicos, o NumPy oferece uma gama de funcionalidades: operações lógicas, manipulação de formatos, ordenação de dados, cálculos estatísticos e até ferramentas para álgebra linear. Não à toa, é considerado a base para outras bibliotecas populares como Pandas, Matplotlib, Scikit-learn e SciPy.
Uma curiosidade interessante do NumPy
Em 10 de abril de 2019, a colaboração do Telescópio Horizonte de Eventos (EHT) revelou a primeira imagem de um buraco negro, localizado no centro da galáxia Messier 87 (M87). Este feito monumental foi o resultado de um esforço colaborativo entre mais de 200 cientistas que utilizaram uma rede global de oito telescópios para coletar dados. O EHT gerou cerca de 350 terabytes de dados em apenas cinco dias, que foram processados ao longo de dois anos. O NumPy esteve presente nesse projeto dando vida a criação da primeira imagem de um buraco negro e a detecção de ondas gravitacionais. Nesse projeto NumPy desempenhou um papel importantíssimo, sendo utilizado para manipular grandes conjuntos de dados e realizar cálculos numéricos necessários para a reconstrução da imagem.
A estrutura de dados n-dimensional do NumPy permitiu que os pesquisadores trabalhassem eficientemente com os dados complexos gerados pelo EHT.

Por que usar o NumPy?
Se você já trabalhou com listas nativas do Python, sabe como elas são versáteis. Mas, quando o assunto é performance e eficiência em operações matemáticas, as listas deixam a desejar. É aí que entra o NumPy, uma ferramenta projetada para lidar com grandes volumes de dados de forma rápida e otimizada.
Imagine ter que realizar cálculos complexos sobre milhões de registros. Com listas comuns, isso pode levar segundos, talvez até minutos. Com o NumPy, esses mesmos cálculos podem ser feitos em milissegundos graças à sua capacidade de vetorização, ou seja, aplicar operações diretamente em arrays inteiros, sem a necessidade de loops.
Além da velocidade, o NumPy também é extremamente eficiente no uso de memória. Comparado às listas do Python, os arrays do NumPy ocupam muito menos espaço, o que significa que você pode trabalhar com conjuntos de dados muito maiores sem se preocupar em sobrecarregar seu sistema.
No curso Introdução à Biblioteca Numpy, da Asimov Academy, você aprenderá a manipular arrays de forma eficiente, explorar as funcionalidades avançadas da biblioteca e dominar operações matemáticas e estatísticas essenciais para análise de dados e ciência de dados. É o primeiro passo para quem deseja construir bases sólidas em Python para aplicações que demandam alto desempenho em manipulação de dados. Confira:

Estruturas de dados no NumPy
O NumPy é uma biblioteca fundamental para a ciência de dados, estatísticas e machine learning em Python, graças à sua capacidade de manipular dados numéricos com extrema eficiência. O elemento central do NumPy é o array, uma estrutura de dados que armazena elementos homogêneos (do mesmo tipo) em uma grade multidimensional, proporcionando vantagens em desempenho e memória em comparação com as listas padrão do Python.
O que são Arrays?
Arrays são estruturas homogêneas, o que significa que todos os elementos contidos nele são do mesmo tipo, como inteiros, pontos flutuantes (floats) ou strings. Eles funcionam como recipientes otimizados para operações matemáticas, permitindo que o NumPy execute cálculos sobre todos os elementos simultaneamente, usando a chamada vetorização.
Essa abordagem elimina a necessidade de loops explícitos no código, resultando em um desempenho muito superior, especialmente ao trabalhar com grandes volumes de dados. Isso faz do NumPy uma escolha indispensável em projetos que requerem eficiência, como análise estatística e processamento de grandes bases de dados.
Dimensões dos Arrays no NumPy
Os arrays podem ser organizados em múltiplas dimensões, conhecidas como eixos.
Arrays unidimensionais
Os arrays unidimensionais, também conhecidos como vetores, são uma coleção linear de elementos. Você pode criar um array unidimensional usando a função np.array() e passando uma lista de elementos que deseja armazenar. Por exemplo, se você quiser criar um array que contenha os números de 1 a 5, siga este exemplo:
import numpy as np
meu_array = np.array([1, 2, 3, 4, 5])
print(meu_array) # Saída: [1 2 3 4 5] Ao imprimir o array, você verá que os elementos estão organizados em uma linha. Além disso, você pode verificar que o tipo de dado retornado é um numpy.ndarray, confirmando que se trata de um array NumPy e não apenas uma lista comum.
Arrays multidimensionais
Se você precisar trabalhar com dados organizados em linhas e colunas, como uma planilha ou uma tabela, os arrays multidimensionais são a melhor opção. Para criar um array bidimensional, você deve fornecer uma lista de listas, onde cada lista interna representa uma linha da matriz:
import numpy as np
meu_array_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(meu_array_2d)
# Saída:
# [[1 2 3]
# [4 5 6]] Neste exemplo, criamos uma matriz de 2 linhas e 3 colunas. Arrays multidimensionais são muito utilizados em situações que exigem organização estruturada de dados, como processamento de imagens, onde cada pixel pode ser representado por um valor em um array bidimensional.
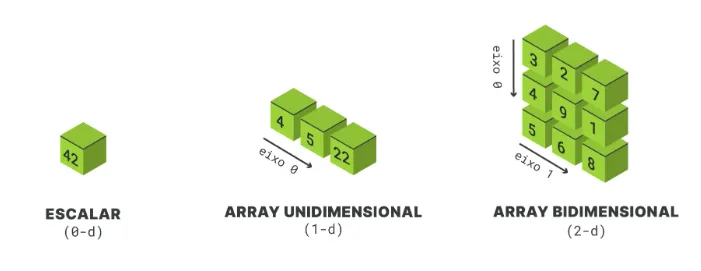
Arrays tridimensionais
Já os arrays tridimensionais são usados para representar dados organizados em três níveis, como uma coleção de matrizes bidimensionais. Isso é particularmente proveitoso em áreas como processamento de imagens, na qual cada camada do array pode representar uma cor (RGB), ou em modelagem científica, como dados climáticos em diferentes altitudes.
Para criar um array tridimensional, você deve passar uma lista de listas de listas para a função np.array(). Veja o exemplo abaixo:
import numpy as np
meu_array_3d = np.array([[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]])
print(meu_array_3d)
# Saída:
# [[[ 1 2 3]
# [ 4 5 6]]
#
# [[ 7 8 9]
# [10 11 12]]]
Neste exemplo, criamos um array com duas matrizes bidimensionais, cada uma contendo duas linhas e três colunas. Ao visualizar o array tridimensional, você perceberá que ele é estruturado em camadas, facilitando a manipulação de grandes conjuntos de dados interligados.
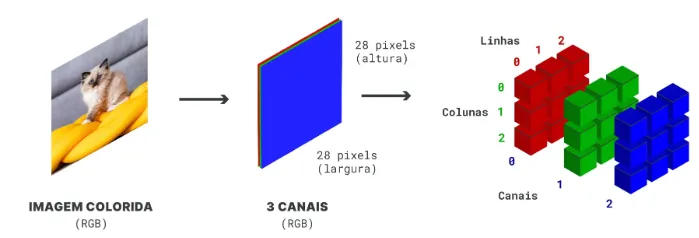
Operações em Arrays com diferentes formatos
Uma das características mais interessantes do NumPy é o broadcasting, que permite realizar operações entre arrays de diferentes tamanhos e formatos, sem a necessidade de fazer ajustes manuais nos dados.
Exemplo prático: soma de uma matriz 2D com um array 1D:
a = np.array([[1, 2], [3, 4]])
b = np.array([10, 20])
resultado = a + b
print(resultado)
Saída:
[[11 22]
[13 24]]
Aqui, o NumPy expande o array unidimensional automaticamente para combinar suas dimensões com a matriz 2D, tornando a operação possível sem precisar reescrever o código.
Como instalar o NumPy?
O NumPy pode ser instalado facilmente utilizando dois métodos populares: pip, o gerenciador de pacotes do Python, e Anaconda, uma distribuição que já inclui várias bibliotecas voltadas para ciência de dados.
Como instalar o NumPy usando Anaconda
O Anaconda é uma plataforma poderosa voltada para ciência de dados, que já vem com diversas bibliotecas pré-instaladas, incluindo o NumPy. Ela se torna ideal para quem deseja um ambiente integrado para Python e R, facilitando o gerenciamento de pacotes e dependências.
Baixe o Anaconda: acesse o site oficial do Anaconda e faça o download para o seu sistema operacional.

Como instalar o Anaconda no Windows
- Instale o NumPy: após instalar o Anaconda, abra o terminal Anaconda Prompt (ou o terminal do seu sistema) e digite:
conda install numpy
- Verifique a instalação: da mesma forma, você pode verificar a instalação abrindo um terminal Python:
import numpy as np
print(np.__version__)
Por que escolher Anaconda?
O Anaconda é recomendado para iniciantes em ciência de dados porque inclui bibliotecas como NumPy, Pandas, Matplotlib, Scikit-learn e Jupyter Notebook pré-configuradas, economizando tempo e evitando conflitos de dependências.
Criando e manipulando arrays
O NumPy oferece uma maneira eficiente de trabalhar com arrays, que são estruturas de dados fundamentais em várias áreas de computação, como ciência de dados, álgebra linear e processamento de imagem. Vamos explorar como acessar, modificar, e manipular dados dentro desses arrays, que podem ser unidimensionais, bidimensionais ou até tridimensionais.
Acessando e modificando elementos em Arrays
O acesso aos elementos de um array é feito por meio de índices. No NumPy, os índices começam em 0, ou seja, o primeiro elemento de um array está no índice 0, o segundo no índice 1 e assim por diante. Para acessar um elemento específico, indique o índice entre colchetes.
Por exemplo, se tivermos o seguinte array unidimensional:
import numpy as np
meu_array = np.array([1, 2, 3, 4, 5])
Para acessar o segundo elemento, você utilizaria o índice 1:
print(meu_array[1]) # Saída: 2
Agora, se você quiser modificar um valor dentro do array, atribua um novo valor ao índice desejado. Por exemplo, se quisermos alterar o segundo valor de meu_array para 10, fazemos:
meu_array[1] = 10
print(meu_array) # Saída: [ 1 10 3 4 5]
Essa capacidade de acessar e modificar elementos permite realizar mudanças rápidas e dinâmicas nos dados com facilidade, o que é útil em muitos cenários, como quando estamos ajustando parâmetros ou realizando operações sobre grandes conjuntos de dados.
Fatiamento e indexação em Arrays
Uma das funcionalidades mais poderosas do NumPy é o fatiamento de arrays. Fatiamento significa que você pode extrair partes específicas de um array sem precisar alterar o array original. Para isso, você pode usar a notação de “slice” (fatia), que permite definir um intervalo de índices.
Por exemplo, se quisermos extrair os três primeiros elementos de meu_array, podemos usar a seguinte sintaxe:
print(meu_array[:3]) # Saída: [1 10 3]
Nesse exemplo, meu_array[:3] retorna os elementos do índice 0 até o índice 2 (o índice 3 não é incluso). Esse tipo de operação é muito útil quando precisamos acessar subarrays ou realizar operações parciais sobre dados, como filtrar ou modificar subconjuntos de grandes coleções de números.
Você também pode fazer fatiamentos mais complexos, por exemplo, extraindo cada segundo elemento de um array:
print(meu_array[::2]) # Saída: [ 1 3 5]
Aqui, meu_array[::2] seleciona todos os elementos com um passo de 2, ou seja, o primeiro, o terceiro e o quinto elementos.
Operações matemáticas com NumPy
O NumPy oferece uma ampla gama de funções que permitem calcular estatísticas básicas, realizar operações entre arrays e até mesmo executar cálculos mais complexos, como álgebra linear. Algumas dessas operações são:
Funções universais: soma, média, máximo e mínimo
O NumPy possui funções que facilitam o cálculo de operações simples, como soma, média, máximo e mínimo, em arrays. Essas operações podem ser aplicadas de maneira direta e retornam os resultados de forma muito rápida, mesmo em grandes volumes de dados.
Soma: para somar todos os elementos de um array, você pode usar a função np.sum():
import numpy as np
meu_array = np.array([1, 2, 3, 4, 5])
print(np.sum(meu_array)) # Saída: 15
Média: para calcular a média dos elementos, utilize a função np.mean():
print(np.mean(meu_array)) # Saída: 3.0
Máximo: para encontrar o maior valor do array, você pode usar np.max():
print(np.max(meu_array)) # Saída: 5
Mínimo: da mesma forma, a função np.min() encontra o menor valor:
print(np.min(meu_array)) # Saída: 1
Essas funções são extremamente úteis quando precisamos obter rapidamente uma visão geral dos dados em nossos arrays.
Operações entre arrays: adição, subtração, multiplicação e divisão
O NumPy permite realizar operações matemáticas entre arrays de maneira simples e intuitiva. Essas operações são elementares, ou seja, ocorrem entre os elementos correspondentes dos arrays.
Por exemplo, se tivermos dois arrays a e b:
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
Podemos realizar as seguintes operações:
Adição:
print(a + b) # Saída: [5 7 9]
Subtração:
print(a – b) # Saída: [-3 -3 -3]
Multiplicação:
print(a * b) # Saída: [4 10 18]
Divisão:
print(a / b) # Saída: [0.25 0.4 0.5]
Essas operações são realizadas de maneira eficiente, aproveitando a estrutura otimizada do NumPy, o que as torna ideais para manipulação de grandes volumes de dados, como em modelos de machine learning ou análises numéricas.
Funções de álgebra linear e estatísticas
Além das operações básicas, o NumPy também possui funções avançadas para realizar cálculos de álgebra linear e estatísticas. Algumas dessas funções são essenciais para resolver problemas mais complexos envolvendo matrizes e vetores.
Transposta de uma matriz: para calcular a transposta de uma matriz, você pode usar a propriedade .T do NumPy. A transposta de uma matriz é uma nova matriz obtida trocando suas linhas por colunas (e vice-versa). Por exemplo:
matriz = np.array([[1, 2], [3, 4]])
print(matriz.T) # Saída: [[1 3] [2 4]]
A transposta de uma matriz é uma operação fundamental em álgebra linear e é frequentemente utilizada em métodos de resolução de sistemas de equações lineares, análise de dados e aprendizado de máquina.
Quer dar o primeiro passo para dominar Python e trabalhar com dados?
Se você está iniciando sua jornada em Python e deseja se tornar proficiente na análise de dados, o curso gratuito Python para Dados, da Asimov Academy, é a oportunidade perfeita. Nele, você aprenderá desde o básico da programação em Python até a criação de gráficos e insights valiosos, podendo praticar com dados reais do Portal da Transparência.
Matricule-se agora e acelere seu aprendizado com conteúdo direto ao ponto, utilizando ferramentas como Pandas.

Python para dados: do zero à análise completa
Cursos de programação gratuitos com certificado
Aprenda a programar e desenvolva soluções para o seu trabalho com Python para alcançar novas oportunidades profissionais. Aqui na Asimov você encontra:
- Conteúdos gratuitos
- Projetos práticos
- Certificados
- +20 mil alunos e comunidade exclusiva
- Materiais didáticos e download de código









Comentários
30xp