Como Calcular o Coeficiente de Correlação Linear em Python

A análise de dados é uma parte fundamental de muitos setores da indústria e da ciência. Uma das análises mais comuns é a correlação linear entre duas variáveis, que pode nos dizer o quanto uma variável está relacionada com a outra. Neste tutorial, vamos aprender a calcular o coeficiente de correlação linear em Python, entendendo a diferença entre os coeficientes de correlação de Pearson e de Spearman.

Curso Gratuito

Seu primeiro projeto Python – curso grátis com certificado!

Vá do zero ao primeiro projeto em apenas 2 horas com o curso Python para Iniciantes.

Comece agora

Entendendo a Correlação

Antes de mergulharmos no código, é importante entender o que é correlação. Imagine que você tem duas variáveis: o número de horas estudadas e as notas de um aluno. Intuitivamente, esperamos que quanto mais um aluno estuda, melhores são suas notas. A correlação nos ajuda a quantificar essa relação. E o valor que quantifica a correlação é justamente o coeficiente de correlação.

Existem diferentes maneiras de calcular o coeficiente de correlação, cada um possuindo uma interpretação específica. Os coeficientes mais comuns são o coeficiente de correlação de Pearson e de Spearman. Ambos coeficientes são valores que variam entre -1 a 1, com o seguinte significado:

• Um coeficiente com valor 1 indica uma correlação positiva perfeita (quando uma variável aumenta, a outra também aumenta na mesma proporção).
• Um coeficiente com valor 0 indica que não há correlação linear.
• Um coeficiente com valor -1 indica uma correlação negativa perfeita (quando uma variável aumenta, a outra diminui na mesma proporção).

Correlação de Pearson

A correlação de Pearson mede a força de uma relação linear entre duas variáveis. Imagine que tenhamos os seguintes dados de horas de estudo e a respectiva nota na prova (em um DataFrame do pandas):

import pandas as pd

dados = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 7, 7.5, 8]
})
print(dados)

# output:
#    horas_estudadas  notas
# 0                1    6.0
# 1                2    6.5
# 2                3    7.0
# 3                4    7.5
# 4                5    8.0

Intuitivamente, conseguimos observar que cada uma hora de estudo adicional aumenta exatamente 0,5 na nota da prova. Isso configura uma correlação linear positiva perfeita, com coeficiente de correlação de Pearson igual a 1.0.

Se colocarmos os pontos em um gráfico do matplotlib, vemos que formam uma linha reta ascendente — mais um indício da correlação linear de Pearson perfeita:

import matplotlib.pyplot as plt
import pandas as pd

dados = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 7, 7.5, 8]
})

# Plota linha
plt.plot(dados['horas_estudadas'], dados['notas'])

# Plota pontos 
plt.scatter(dados['horas_estudadas'], dados['notas'])

plt.show()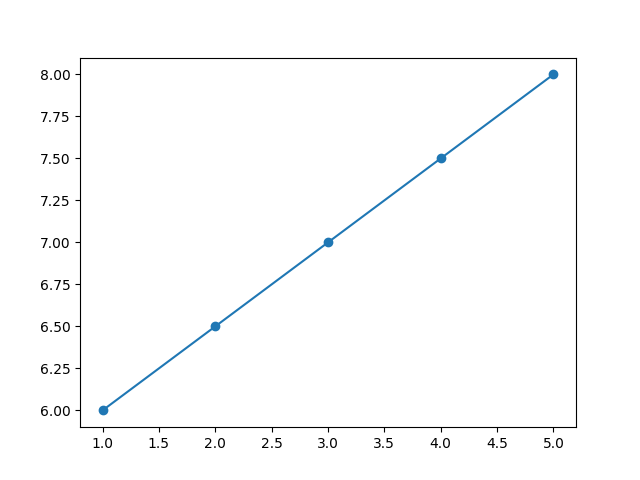

Correlação de Spearman

E se a relação não for tão perfeita assim? Vamos avaliar agora um novo conjunto de dados:

import pandas as pd

dados_mod = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 6.8, 6.95, 7]
})
print(dados_mod)

# output:
#    horas_estudadas  notas
# 0                1   6.00
# 1                2   6.50
# 2                3   6.80
# 3                4   6.95
# 4                5   7.00

Por mais que a conclusão seja a mesma — quanto mais horas de estudo, maior a nota — vemos que a relação não é mais “perfeita”: a segunda hora de estudo adicionou 0,5 à nota da prova, porém a terceira hora adicionou apenas 0,3. A relação de mais 1 hora de estudo para mais 0,5 de nota na prova foi parcialmente perdida. Isso fica visível na análise gráfica, onde não há mais uma linha reta ascendente:

import matplotlib.pyplot as plt
import pandas as pd

dados_mod = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 6.8, 6.95, 7]
})

# Plota linha
plt.plot(dados_mod['horas_estudadas'], dados_mod['notas'])

# Plota pontos 
plt.scatter(dados_mod['horas_estudadas'], dados_mod['notas'])

plt.show()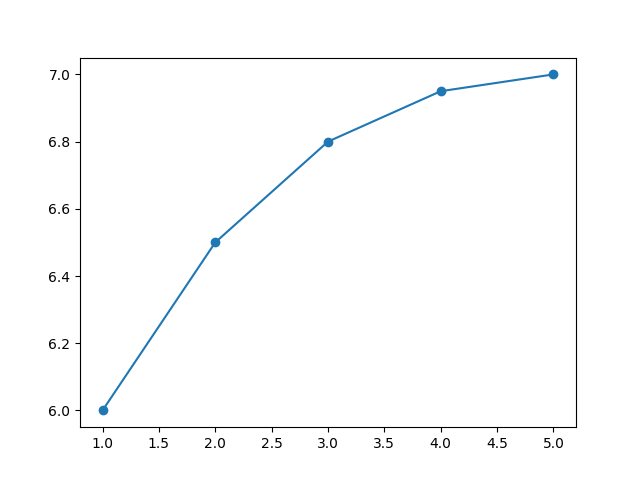

Mesmo assim, sabemos que existe ainda alguma relação positiva entre as variáveis, mesmo que tal relação não siga um aumento constante. Nestes casos, pode fazer sentido usar o coeficiente de correlação de Spearman.

O coeficiente de correlação de Spearman é baseada no “rank” das variáveis, e não nos valores exatos. Isto significa que a correlação continua sendo “perfeita” desde que os maiores valores da variável A estejam associados aos maiores valores da variável B — independente do valor numérico de ambas variáveis.

Fazendo uma analogia: é como se estivéssemos avaliando se os melhores corredores são também os melhores nadadores, olhando apenas para sua posição no pódio (primeiro, segundo, terceiro) ao invés de medir sua velocidade na corrida ou natação.

Em termos técnicos, o fato de a correlação de Spearman usar o rank das variáveis no lugar de seu valor faz com que ela seja considerada a versão não paramétrica da correlação de Pearson.

Calculando a Correlação em Python

Agora que temos uma compreensão básica do que são as correlações de Pearson e Spearman, vamos ver como calcular os seus respectivos coeficientes de correlação em Python.

A biblioteca scipy (nome derivado do inglês scientific Python ou “Python científico”) possui funções prontas para calcular os coeficientes de correlação em Python. Caso você não a possua no seu ambiente, você pode instalá-la com pip:

pip install scipy

Preparando os Dados

Vamos começar importando as bibliotecas e recriando os dois conjunto de dados usados nos exemplos anteriores:

import pandas as pd
from scipy.stats import pearsonr, spearmanr

dados = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 7, 7.5, 8]
})

dados_mod = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 6.8, 6.95, 7]
})

Calculando o Coeficiente de Correlação de Pearson em Python

Para calcular a correlação de Pearson, usamos a função pearsonr do scipy.stats. Os argumentos da função são as duas colunas do DataFrame para as quais queremos calcular o coeficiente de correlação:

# Calculando a correlação de Pearson para DataFrame "dados"
coef_pearson, p_valor = pearsonr(dados['horas_estudadas'], dados['notas'])

print(coef_pearson)
# output: 1.0

# Calculando a correlação de Pearson para DataFrame "dados_mod"
coef_pearson, p_valor = pearsonr(dados_mod['horas_estudadas'], dados_mod['notas'])

print(coef_pearson)
# output: 0.9395

Calculando o Coeficiente de Correlação de Spearman em Python

De maneira semelhante, podemos calcular a correlação de Spearman com a função spearmanr:

# Calculando a correlação de Spearman para DataFrame "dados"
coef_spearman, p_valor = spearmanr(dados['horas_estudadas'], dados['notas'])

print(coef_spearman)
# output: 0.99999999

# Calculando a correlação de Spearman para DataFrame "dados_mod"
coef_spearman, p_valor = spearmanr(dados_mod['horas_estudadas'], dados_mod['notas'])

print(coef_spearman)
# output: 0.99999999

Interpretando os Resultados

Tanto a função pearsonr quanto spearmanr retornam dois valores. O primeiro valor é o coeficiente de correlação propriamente dito. Já o segundo valor é o chamado p-valor — uma medida estatística que informa a chance do resultado da correlação ser fruto do acaso (e não de uma correlação de fato). Neste artigo não nos aprofundaremos sobre o p-valor, mas é importante saber que podemos obtê-lo dessa forma.

Veja que os valores dos coeficientes de correlação estão de acordo com o que discutimos anteriormente: o coeficiente de correlação de Pearson tem valor 1.0 apenas quando os dados possuem uma relação linear. Ao calcularmos o coeficiente de correlação para o conjunto de dados dados_mod, obtivemos o valor 0.939 — indicando uma correlação alta, mas não perfeita.

Por outro lado, o coeficiente de correlação de Spearman foi de 1.0 em ambos os casos porque o maior valor de uma variável estava sempre associado ao maior valor da outra, independente dos valores em si. (Na realidade, o valor foi de 0.99999999…, mas isto é apenas decorrente da imprecisão natural de números decimais em computadores).

Código completo

import pandas as pd
from scipy.stats import pearsonr, spearmanr

dados = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 7, 7.5, 8]
})

dados_mod = pd.DataFrame({
    'horas_estudadas': [1, 2, 3, 4, 5],
    'notas': [6, 6.5, 6.8, 6.95, 7]
})

# Calculando a correlação de Pearson para DataFrame "dados"
coef_pearson, p_valor = pearsonr(dados['horas_estudadas'], dados['notas'])

print(coef_pearson)
# output: 1.0

# Calculando a correlação de Pearson para DataFrame "dados_mod"
coef_pearson, p_valor = pearsonr(dados_mod['horas_estudadas'], dados_mod['notas'])

print(coef_pearson)
# output: 0.9395

# Calculando a correlação de Spearman para DataFrame "dados"
coef_spearman, p_valor = spearmanr(dados['horas_estudadas'], dados['notas'])

print(coef_spearman)
# output: 0.99999999

# Calculando a correlação de Spearman para DataFrame "dados_mod"
coef_spearman, p_valor = spearmanr(dados_mod['horas_estudadas'], dados_mod['notas'])

print(coef_spearman)
# output: 0.99999999

Conclusão

Neste tutorial, aprendemos a diferença entre os coeficientes de correlação de Pearson e Spearman e como calculá-los em Python. Essas técnicas são fundamentais para a análise de dados e podemos aplicá-las em uma variedade de campos, desde a ciência até o mundo dos negócios.

Agora que você tem o conhecimento básico, pode começar a explorar seus próprios conjuntos de dados e descobrir as relações interessantes que eles podem conter!