Análise de Correlação Linear em Python

A análise de correlação linear é uma ferramenta estatística que avalia o quanto duas variáveis estão relacionadas. Se você está começando a explorar o mundo da análise de dados em Python, é fundamental que você aprenda a criar uma análise de correlação linear em Python.

O Conceito de Correlação Linear

Imagine que você está analisando o desempenho de vendas de uma loja de sorvetes. Você se pergunta: será que as vendas de sorvete aumentam quando faz calor? Em outras palavras, será que há relação entre a temperatura média do dia e quantidade de sorvete vendido?

Se, em dias mais quentes, as vendas de sorvete aumentam, dizemos que há uma correlação positiva entre as variáveis “temperatura média” e “quantidade de sorvete vendido”. Por outro lado, se em dias mais quentes, as vendas de sorvete diminuem, temos uma correlação negativa entre essas variáveis.

A correlação linear é geralmente representada por um valor no intervalo -1 e 1, conhecido como coeficiente de correlação. Um valor próximo de 1 indica uma forte correlação positiva, enquanto um valor próximo de -1 indica uma forte correlação negativa. Um valor próximo de 0 sugere que não há correlação linear entre as variáveis, isto é, o aumento de uma das variáveis não implica nem no aumento, nem na diminuição da outra.

Exemplos de Correlação Linear em Python

Para explorar a correlação linear, vamos usar a biblioteca pandas para manipulação de dados e a biblioteca matplotlib para visualização. Primeiro, precisamos instalar essas bibliotecas, caso ainda não estejam instaladas:

pip install pandas matplotlib

Agora, vamos ao código:

Importando as Bibliotecas

import pandas as pd
import matplotlib.pyplot as plt

Criando um DataFrame

Vamos criar um DataFrame simples para ilustrar a correlação linear:

# Dados de exemplo
dados = {
    'Temperatura': [25, 30, 20, 35, 32],
    'Vendas': [300, 400, 350, 500, 450]
}

# Criando um DataFrame
df = pd.DataFrame(dados)

# Mostrando o DataFrame
print(df)

# output:
#          Temperatura  Vendas
# 0                 25     300
# 1                 30     400
# 2                 20     350
# 3                 35     500
# 4                 32     450

Calculando a Correlação

Para calcular a correlação, usamos o método corr() do DataFrame:

# Calculando a correlação
correlacao = df.corr()
print(correlacao)

#              Temperatura    Vendas
# Temperatura     1.000000  0.851594
# Vendas          0.851594  1.000000

Vemos que a correlação entre temperatura e vendas é aproximadamente 0.85, o que é uma correlação positiva alta (próxima de 1.0). Isso significa que sim, o aumento na temperatura média do dia faz com que a quantidade de sorvete vendido também aumente!

O DataFrame retornado pelo método corr() possui as variáveis tanto nas linhas quanto nas colunas. Cada cruzamento de linha e coluna representa a correlação entre as duas variáveis, formando assim uma matriz de correlação.

Note que essa matriz é “espelhada”, porque a ordem de fatores não altera o resultado: calcular a correlação de A com B é a mesma coisa que calcular a correlação de B com A. Além disso, a diagonal principal sempre demonstra a correlação de cada variável consigo mesmo, o que sempre será 1.

Visualizando a Correlação

Uma maneira eficaz de visualizar a correlação é através de um gráfico de dispersão:

# Plotando o gráfico de dispersão
plt.scatter(df['Temperatura'], df['Vendas'])
plt.title('Correlação entre temperatura média do dia e vendas de sorvete')
plt.xlabel('Horas Trabalhadas')
plt.ylabel('Temperatura')
plt.show()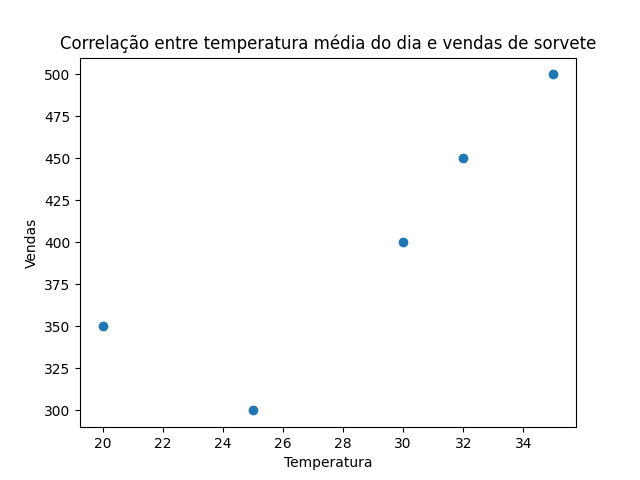

Este gráfico nos ajudará a visualizar a relação entre as horas trabalhadas e as vendas. Se os pontos formarem uma linha ascendente da esquerda para a direita, isso indica uma correlação positiva.

Conclusão

A análise de correlação linear é uma técnica poderosa que nos permite identificar relações entre variáveis e tomar decisões informadas com base em dados. Realizar a análise de correlação linear com Python é simples e eficaz, permitindo que mesmo iniciantes possam extrair insights valiosos de seus dados.