K-means: o que é e como usar na prática com Python

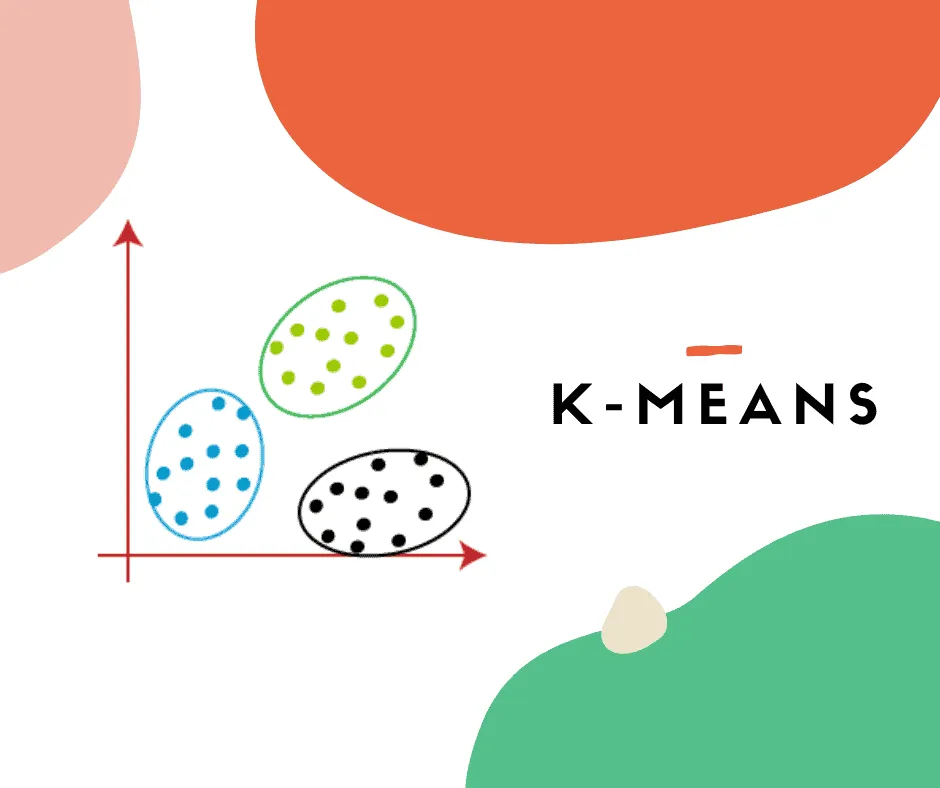
O K-means é um algoritmo de aprendizado não supervisionado utilizado para clusterização, ou seja, para agrupar dados semelhantes em conjuntos chamados clusters. O nome vem do fato de trabalhar com K, que é o número de clusters definidos previamente pelo usuário, e means, que se refere à média dos pontos de dados em cada cluster, representada pelo centróide (a média dos pontos dentro do cluster).

O objetivo principal do K-means é particionar os dados em K grupos, de modo que os dados dentro de cada cluster sejam mais próximos entre si do que em relação aos dados de outros clusters, para minimizar a soma das distâncias quadradas entre os pontos e seus respectivos centróides.

O funcionamento básico do algoritmo ocorre de forma iterativa, em dois passos principais:

• Atribuição: cada ponto de dado é atribuído ao cluster cujo centróide está mais próximo, geralmente utilizando a distância euclidiana como medida;
• Atualização: recalcula-se o centróide de cada cluster como a média de todos os pontos atribuídos a ele.

Esses passos se repetem até que os centróides se estabilizam (não mudam mais) ou até que um número máximo de iterações seja atingido.

Por ser um método simples, eficiente e eficaz, o K-means é utilizado em várias áreas, como segmentação de mercado, agrupamento de documentos, segmentação e compressão de imagens, entre outras aplicações em ciência de dados.

Clusterização e segmentação de universidades americanas

Como funciona o algoritmo K-means?

Como mostrado, o K-means é um método simples e eficiente para agrupar dados em K grupos (clusters) com base em semelhança normalmente medida por distância.Ele alterna entre atribuir pontos ao centro mais próximo, e recalcular esses centros até estabilizar. Abaixo está o fluxo completo, explicado de forma direta.

Passo a passo

1. Escolher K (número de clusters)
   Você decide quantos grupos quer formar. Em muitos casos, K-means é definido com base no contexto do problema ou por técnicas como método do “cotovelo” ou pontuação silhouette.
   
2. Inicializar centróides
   Selecionam-se K posições iniciais no espaço dos dados. A forma mais simples é escolher pontos reais do conjunto de forma aleatória. Métodos como k-means++ escolhem os melhores pontos iniciais para reduzir o risco de resultados ruins.
   
3. Atribuir cada ponto ao centróide mais próximo
   Para cada ponto, calcula-se a distância (com frequência, distância euclidiana) até todos os centróides e o ponto é associado ao cluster cujo centro está mais perto.
   
4. Recalcular os centróides
   Para cada cluster, calcula-se a média (componente a componente) de todos os pontos atribuídos a ele. Essa média se torna o novo centróide.
   
5. Repetir (atribuir → recalcular) até convergir
   O algoritmo alterna entre atribuição e atualização de centróides até que:
   
   • as atribuições deixem de mudar, ou
     
   • o deslocamento dos centróides fique abaixo de um limite, ou
     
   • seja atingido um número máximo de iterações previamente definido.

Métodos do K-means mais usados para escolha do K ideal

Quando chegamos à etapa de definir quantos grupos (K) o K-means deve criar, não existe fórmula mágica: é preciso equilibrar objetividade e bom senso. A seguir, apresento seis abordagens consolidadas, cada uma com suas vantagens, exemplos de código e dicas de visualização. Escolher o melhor método ou combiná-los ajuda a encontrar o valor de K que faz sentido para os seus dados.

1. Método do Cotovelo (Elbow Method)

Você calcula a inércia (soma dos quadrados das distâncias entre cada ponto e o centróide do seu cluster) para diferentes valores de K. Ao plotar a inércia em função de K, o gráfico geralmente se “dobrará” em um ponto: esse “cotovelo” sugere onde ganhos adicionais passam a ser menores.

inertias = []
for k in range(1, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    inertias.append(km.inertia_)
plt.plot(range(1, 11), inertias, 'o-')

inertias = []
for k in range(1, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    inertias.append(km.inertia_)
plt.plot(range(1, 11), inertias, 'o-')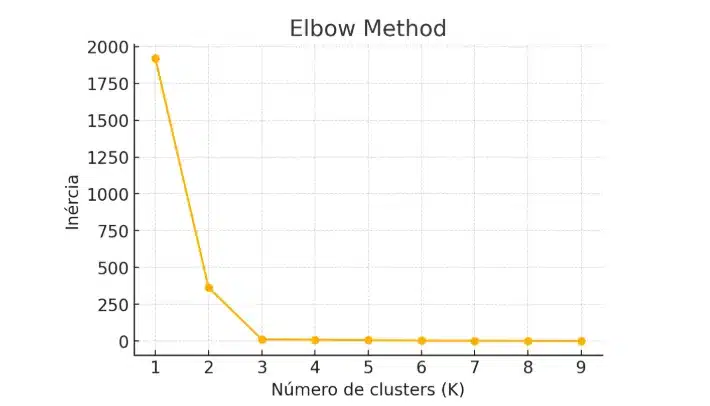

2. Silhouette Score

Esse índice avalia, para cada ponto, o quanto ele está próximo do seu próprio cluster em relação ao mais próximo:

s(i) = (b(i) – a(i)) / max{a(i), b(i)}

• a(i) = distância média ao seu cluster;
  

b(i) = menor distância média a outro cluster.
Valores próximos de 1 mostram grupos bem separados, valores perto de 0 indicam áreas de transição e negativos expõem pontos mal alocados. É só calcular o score para vários K-means e escolher aquele que maximize o valor.

scores = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    scores.append(silhouette_score(X, km.labels_))
plt.plot(range(2,11), scores, 'o-')

scores = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    scores.append(silhouette_score(X, km.labels_))
plt.plot(range(2,11), scores, 'o-')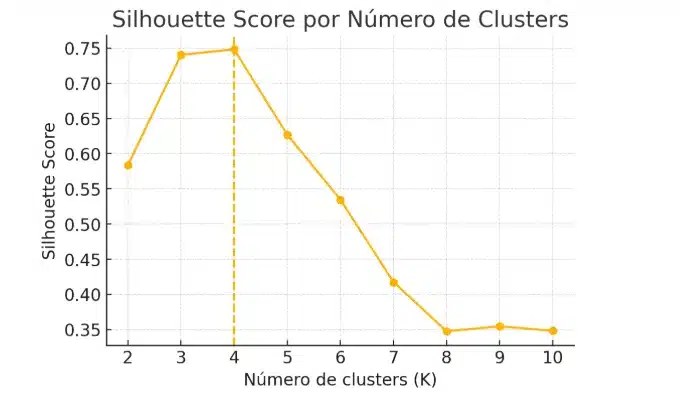

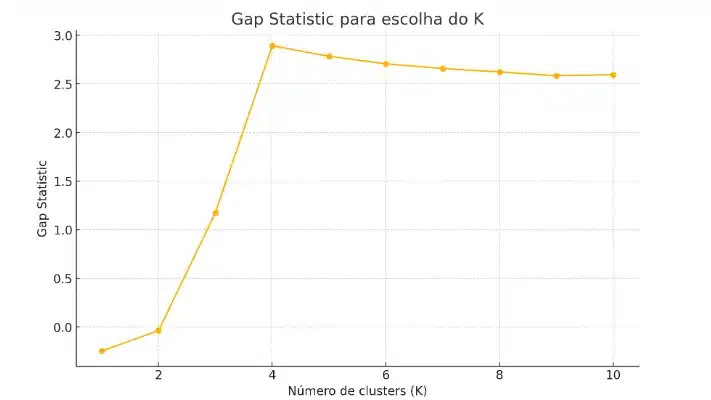
3. Gap Statistic

Compara a inércia dos clusters sobre os dados reais com a inércia média em dados aleatórios que não apresentam padrão. A diferença (gap) maior indica um K-means que revela estrutura genuína. Embora seja mais pesado computacionalmente, esse método oferece uma visão robusta da relevância dos clusters.

4. Índice de Davies–Bouldin

Mede a relação entre a dispersão intra-cluster e a distância inter-cluster:Quanto menor o valor, melhor a distinção entre grupos.

db = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    db.append(davies_bouldin_score(X, km.labels_))
plt.plot(range(2,11), db, 'o-')

db = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    db.append(davies_bouldin_score(X, km.labels_))
plt.plot(range(2,11), db, 'o-')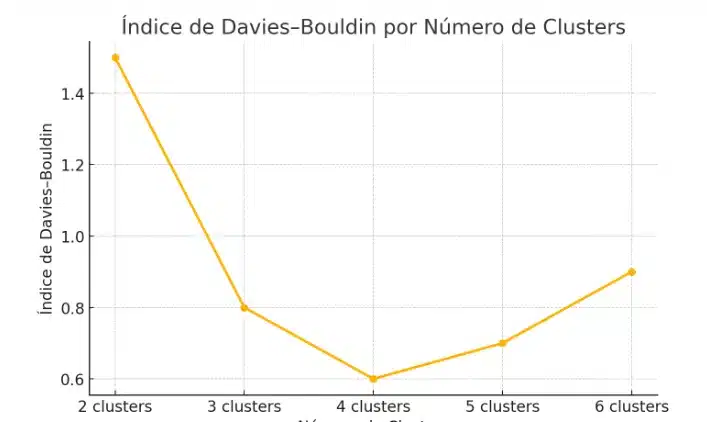

5. Índice Calinski-Harabasz

Também chamado de razão de variância, compara a variabilidade entre clusters com a variabilidade dentro dos clusters. Pontuações mais altas significam que os grupos estão claros e bem formados.

ch = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    ch.append(calinski_harabasz_score(X, km.labels_))
plt.plot(range(2,11), ch, 'o-')

ch = []
for k in range(2, 11):
    km = KMeans(n_clusters=k, random_state=0, n_init=10).fit(X)
    ch.append(calinski_harabasz_score(X, km.labels_))
plt.plot(range(2,11), ch, 'o-')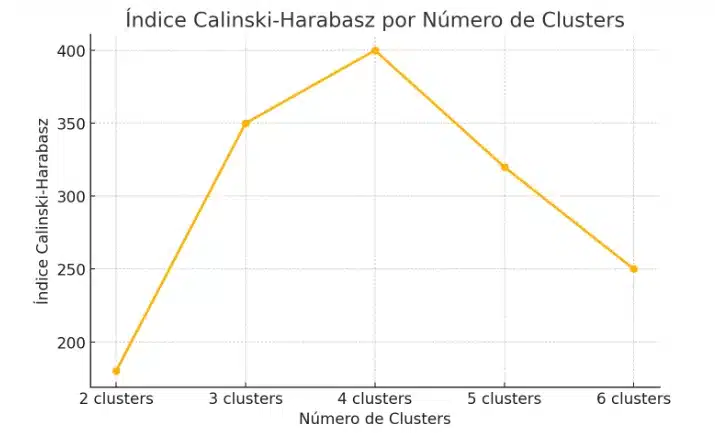

6. Adjusted Rand Index (ARI)

Quando você tem rótulos verdadeiros (ground truth), o ARI mede a similaridade entre a classificação real e a gerada pelo K-means, ajustando para o acaso. Vai de –1 (discordância total) a 1 (perfeita coincidência). Sem rótulos, não serve para escolher K, mas ajuda a avaliar a qualidade do agrupamento.

ari = adjusted_rand_score(y_true, y_pred)

ari = adjusted_rand_score(y_true, y_pred)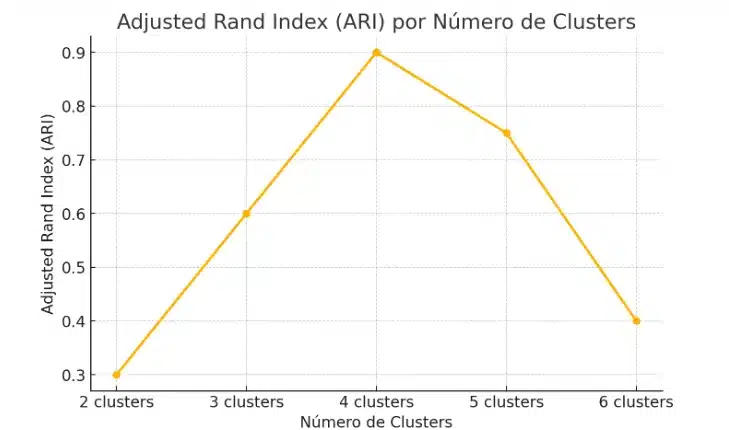

Em geral, Elbow e Silhouette são os primeiros a serem testados por sua simplicidade. Mas combiná-los com métodos como Gap ou Calinski-Harabasz reforça a escolha, especialmente em cenários mais complexos. Ao aplicar esses índices e conferir os gráficos, você terá confiança para definir um K que reflita de fato a estrutura oculta nos seus dados.

Vantagens e desvantagens do K-means

K‑means ganhou popularidade porque entrega segmentações rápidas com pouco esforço, mas ele também faz suposições fortes sobre a forma dos dados. Entender onde brilha e onde falha ajuda você a escolher o algoritmo certo (ou a ajustar os dados antes de usá-lo). Veja os principais pontos.

Vantagens do K-means

• Simples e rápido: fácil de entender, poucas linhas de código e ótima performance mesmo em bases grandes, especialmente com implementações otimizadas (como a do scikit-learn ou MiniBatchKMeans);
  
• Bom para grupos “esféricos”: quando os dados formam aglomerados relativamente compactos e de tamanho parecido, o K‑means tende a encontrar centros representativos;
  
• Escalável: o custo cresce de forma razoável com o número de amostras e dimensões; versões em lote ou distribuídas permitem uso em milhões de registros;
  
• Sempre converge: cada iteração reduz (ou mantém) a soma dos erros quadráticos internos; o processo termina em poucas rodadas. O resultado pode ser local, mas é estável;
  
• Base para extensões: serve como etapa inicial ou componente em técnicas mais avançadas: inicialização para Gaussian Mixture Models, compressão de dados (vector quantization), agrupamento de pixels em visão computacional, entre outras.

Desvantagens do K-means

• Sensível a outliers: pontos extremos puxam o centróide;
• Precisa de K antecipado: escolher o número de clusters antes do treino pode ser arbitrário; 
• Supõe forma e tamanho parecidos: clusters alongados, irregulares ou com densidades diferentes tendem a ser mal representados; 
• Dependente da inicialização: centros ruins levam a soluções ruins (mínimos locais);
• Desequilíbrio de tamanhos: clusters grandes podem “engolir” pequenos, porque o objetivo minimiza erros globais.

7 Principais aplicações do K-means

Quando temos muitos dados e queremos descobrir quem se parece com quem, o K-means costuma ser uma das primeiras tentativas. Ele separa pontos em grupos (clusters) com base na proximidade, de modo simples e rápido, tornando padrões mais claros para quem precisa agir sobre eles. A seguir, veja onde ele aparece com mais frequência e por que faz sentido usar.

1. Segmentação de clientes

Em marketing e CRM, o K-means ajuda a dividir a base de clientes em grupos com comportamentos parecidos: frequência e valor de compra, preferências de produtos, estágio no ciclo de vida, faixa de renda, localização e muito mais. Com isso, campanhas podem ser personalizadas, ofertas são direcionadas, e fica mais fácil medir retorno sobre investimento por segmento.

2. Segmentação e compressão de imagens

No processamento de imagens, o algoritmo agrupa pixels por cor ou textura, permitindo recortes automáticos de objetos, mapas de regiões semelhantes e redução de paletas para compressão. É útil em visão computacional, edição de imagens e aplicações que precisam simplificar arquivos sem perder o que importa visualmente.

3. Agrupamento de dados genéticos e expressão gênica

Em biologia e bioinformática, o K-means agrupa genes ou amostras com perfis de expressão semelhantes. Isso apoia a descoberta de biomarcadores, a identificação de vias biológicas relacionadas e a comparação entre condições (por exemplo, tecido saudável ou doente).

4. Organização de textos e documentos

Ao transformar textos em vetores numéricos (por embeddings, TF‑IDF etc.), podemos usar K-means para reunir documentos parecidos: artigos sobre o mesmo assunto, tickets de suporte com problemas semelhantes, conteúdos a moderar, ou coleções extensas que precisam de rótulos iniciais para navegação e busca mais inteligente.

5. Sistemas de recomendação

Agrupar usuários com hábitos parecidos ou itens consumidos por públicos semelhantes ajuda a iniciar ou complementar mecanismos de recomendação. Em plataformas com catálogos enormes, clusters podem guiar ofertas básicas antes de modelos mais sofisticados entrarem em cena ou servir como uma camada de segmentação adicional.

6. Análise exploratória e preparação de dados

Antes de treinar modelos supervisionados, muitas equipes usam K-means para entender a estrutura dos dados: detectar padrões brutos, reduzir complexidade, criar variáveis derivadas (distância ao centróide, ID do cluster) ou descobrir subgrupos que merecem modelagens separadas.

7. Detecção de padrões em domínios variados

O mesmo raciocínio vale para dados de finanças (perfis de risco, comportamentos de gasto), saúde (grupos de pacientes com sinais semelhantes), geolocalização (zonas de mobilidade ou tráfego), IoT e sensores industriais (equipamentos com leituras parecidas que podem indicar estado comum). Sempre que precisamos encontrar agrupamentos naturais para apoiar decisões específicas, o K-means pode ajudar.

Agora é a hora de colocar o K-means em prática!

Você já entendeu como o K-means funciona e viu como essa técnica pode te ajudar a segmentar dados e revelar padrões. Agora imagine dominar não só o K-means, mas também outras ferramentas de Machine Learning para transformar dados em decisões estratégicas e resultados reais.

Na Trilha Data Science e Machine Learning da Asimov Academy, você encontra tudo o que precisa para sair do zero e construir projetos que realmente fazem diferença:

• Exercícios práticos com Python para aplicar imediatamente o que você aprendeu;
  
• Casos reais que simulam desafios enfrentados por cientistas de dados no mercado;
  
• Mentorias e dicas exclusivas para acelerar seu aprendizado;
  
• Acesso a uma comunidade de profissionais e entusiastas que estão evoluindo junto com você.

Se você está cansado de apenas ler sobre algoritmos e quer ver seus códigos rodando e gerando insights reais, essa trilha é o passo que falta.

Trilha Data Science e Machine Learning

Explore dados, desenvolva modelos preditivos e extraia insights valiosos para impulsionar a tomada de decisões.

Comece agora