Regressão Linear: conceitos fundamentais e aplicações práticas

 A regressão linear é uma das técnicas estatísticas mais essenciais e amplamente usadas em ciência de dados. Sua simplicidade e eficácia a tornam ideal para modelar relações entre variáveis, ajudando a prever resultados e entender como diferentes fatores influenciam um determinado resultado. Neste artigo, vamos explorar os conceitos fundamentais da regressão linear, desde suas bases matemáticas até suas aplicações práticas em áreas como negócios, saúde e ciências sociais. 

Além disso, você aprenderá como implementar a regressão linear utilizando Python, uma das linguagens mais poderosas para análise de dados. Vamos mergulhar no universo dessa técnica que transforma dados em insights valiosos.

O que é regressão linear?

A regressão linear é uma técnica estatística usada para modelar a relação entre uma variável dependente e uma ou mais variáveis independentes. Uma regressão linear ajuda a encontrar a melhor linha reta que representa um conjunto de dados, permitindo prever resultados futuros com base em informações existentes. Por sua simplicidade e eficácia, é amplamente aplicada em áreas como economia, biologia e ciências sociais.

A regressão linear é uma ferramenta indispensável na ciência de dados, pois oferece uma forma clara de entender como diferentes fatores influenciam um resultado. Imagine um gestor analisando o impacto do investimento em publicidade nas vendas de um produto: com a regressão linear, ele consegue traduzir dados em insights práticos. É justamente essa capacidade de tornar os números mais compreensíveis e úteis que faz dessa técnica uma das mais valorizadas.

Regressão Logística em dados de publicidade

Por que a regressão linear é importante?

A regressão linear é uma das ferramentas mais populares em várias áreas de pesquisa, principalmente por ser rápida, fácil de interpretar e extremamente versátil.

Ela permite transformar dados em análises valiosas, simulando diferentes tipos de relações entre variáveis. Além disso, sua simplicidade em comparação com métodos mais complexos, como redes neurais, facilita a análise e comparação de seus parâmetros estatísticos, tornando-a ideal para extrair informações úteis de maneira prática.

Mas a regressão linear não é apenas uma ferramenta de previsão. Ela também é muito eficaz para descrever sistemas e entender como diferentes fatores interagem. Se você precisa modelar uma variável numérica com poucas variáveis independentes e quer um modelo fácil de interpretar, a regressão linear será, provavelmente, sua escolha natural.

Bases matemáticas da regressão linear

Para compreender de fato o que é uma regressão linear, é importante se familiarizar com suas bases matemáticas. A equação fundamental da regressão linear simples é:

Y=β0+β1X+ϵY = \beta_0 + \beta_1X + \epsilonY=β0​+β1​X+ϵ

Onde:

• YYY: variável dependente (o que queremos prever);
• β0\beta_0β0​: interceptação da linha com o eixo Y, ou seja, o valor de YYY quando XXX é zero;
• β1\beta_1β1​: coeficiente que indica a inclinação da linha, mostrando como YYY varia à medida que XXX muda;
• XXX: variável independente (usada para prever YYY);
• ϵ\epsilonϵ: erro aleatório, representando as diferenças entre os valores observados e os previstos.

Interpretação dos parâmetros do modelo

Os parâmetros β0\beta_0β0​ e β1\beta_1β1​ desempenham papéis essenciais na interpretação do modelo:

• β0\beta_0β0​: representa o valor esperado de YYY quando XXX é igual a zero. Por exemplo, se estamos analisando o impacto da temperatura nas vendas de sorvete, β0\beta_0β0​ seria o número de sorvetes vendidos quando a temperatura é zero graus;
• β1\beta_1β1​: mostra a relação entre XXX e YYY. Se β1\beta_1β1​ for igual a 2, significa que para cada aumento de 1 unidade em XXX, YYY aumentará em 2 unidades.

A beleza da regressão linear está em sua simplicidade e clareza: ela traduz relações matemáticas em interpretações práticas, facilitando decisões baseadas em dados.

Tipos de regressão linear

Se você está começando a explorar o mundo da análise de dados, entender os tipos de regressão linear é um passo essencial. Esta técnica estatística ajuda a identificar padrões e fazer previsões baseadas em dados existentes. Vamos começar pelo básico, passando por exemplos práticos que mostram como a regressão linear pode ser aplicada no dia a dia.

1. Regressão linear simples

A regressão linear simples é o ponto de partida para quem quer aprender sobre essa técnica. Ela analisa a relação entre uma variável independente e uma variável dependente, ou seja, entre uma causa e um efeito.

A equação básica é:

Y=β0+β1X+ϵY = \beta_0 + \beta_1X + \epsilonY=β0​+β1​X+ϵ

Componentes principais:

• YYY: a variável dependente, aquilo que queremos prever (exemplo: vendas de um produto);
• XXX: a variável independente, o fator que usamos para prever YYY (exemplo: gastos com publicidade);
• β0\beta_0β0​: o ponto onde a linha de regressão cruza o eixo Y, ou seja, o valor de YYY quando XXX é zero;
• β1\beta_1β1​: a inclinação da linha de regressão, que indica como YYY muda para cada unidade de variação em XXX;
• ϵ\epsilonϵ: o termo de erro, que representa as diferenças entre os valores reais e os previstos.

Exemplo prático

Imagine que você é um agricultor e quer prever a produtividade da sua colheita com base na quantidade de chuva. Nesse caso:

• A quantidade de chuva seria XXX, a variável independente;
• A produtividade da colheita seria YYY, a variável dependente.

Ao usar a regressão linear simples, você pode descobrir, por exemplo, que cada aumento de 10 mm na chuva aumenta a produtividade da colheita em 5%. Essa relação direta entre dois fatores é o que torna a regressão linear simples tão útil.

2. Regressão linear múltipla

À medida que adicionamos mais variáveis independentes, entramos no território da regressão linear múltipla. Aqui, analisamos como vários fatores influenciam um único resultado.

A equação se expande para:

Y=β0+β1X1+β2X2+…+βnXn+ϵY = \beta_0 + \beta_1X_1 + \beta_2X_2 + … + \beta_nX_n + \epsilonY=β0​+β1​X1​+β2​X2​+…+βn​Xn​+ϵ

Componentes adicionais:

• X1,X2,…,XnX_1, X_2, …, X_nX1​,X2​,…,Xn​: variáveis independentes adicionais;
• β1,β2,…,βn\beta_1, \beta_2, …, \beta_nβ1​,β2​,…,βn​: coeficientes que mostram o impacto de cada variável independente em YYY.

Exemplo prático

Pense em um cenário em que você quer prever o preço de uma casa. O valor final depende de vários fatores, como:

• Tamanho da casa (X1X_1X1​);
• Localização (X2X_2X2​);
• Número de quartos (X3X_3X3​);
• Idade do imóvel (X4X_4X4​).

Ao usar a regressão linear múltipla, você pode identificar, por exemplo, que o tamanho da casa influencia mais o preço do que a idade do imóvel. Essa análise permite compreender como cada fator contribui para o resultado final, ajudando na tomada de decisões.

Na videoaula abaixo, o nosso professor Rodrigo Tadewald ensina a utilizar um modelo de regressão para prever o preço justo de aluguel de apartamentos em São Paulo. Os dados utilizados são de uma base pública do Kaggle contendo informações reais de imóveis.

3. Regressão logística

Embora não seja tecnicamente “linear”, a regressão logística é outra ferramenta importante que se baseia em conceitos semelhantes. Ela não se preocupa em prever valores numéricos, mas sim em probabilidades.

Como funciona?

Em vez de uma linha reta, a regressão logística usa uma curva em formato de “S” para prever se algo vai ou não acontecer. O resultado é sempre um valor entre 0 e 1:

• 0 significa que o evento é muito improvável;
• 1 significa que o evento é quase certo de acontecer.

A equação usa uma função logarítmica para calcular essa probabilidade.

Exemplo prático

• Prever a chance de um cliente fazer ou não uma compra online;
• Determinar se um paciente tem ou não uma determinada doença com base em seus exames;
• Identificar se uma imagem contém um gato ou um cachorro.

Programas para análise de regressão linear

Para quem deseja realizar análises de regressão linear, existem diversos softwares que tornam o processo mais simples e acessível, mesmo para iniciantes. Abaixo, apresentamos alguns dos principais programas gratuitos disponíveis, com destaque para suas funcionalidades e compatibilidade com diferentes sistemas operacionais.

1. JASP

O JASP é uma excelente opção gratuita para quem precisa realizar análises de regressão. Com um design intuitivo e módulos específicos para várias técnicas de análise estatística, ele é ideal para explorar as variáveis que afetam determinado tema ou área de interesse.

Características principais:

• Disponível para Windows e Mac;
• Suporte a vários métodos de regressão, como simples e múltipla;
• Interface amigável, ideal tanto para iniciantes quanto para usuários mais experientes.

2. PSPP

O PSPP é uma alternativa gratuita ao popular software SPSS, com funcionalidades robustas para análise estatística e regressão linear. Ele é particularmente útil para quem trabalha com diferentes sistemas operacionais.

Características principais:

• Compatível com Windows, Mac, Ubuntu, FreeBSD e outros sistemas;
• Permite inserir conjuntos de dados facilmente e realizar análises detalhadas;
• Os resultados são apresentados em uma interface de visualização clara, com todos os passos da análise bem documentados.

Dica de uso:

Se você está acostumado ao SPSS, o PSPP é uma ótima opção para quem busca uma solução gratuita, com uma curva de aprendizado suave.

3. Statcato

O Statcato é uma ferramenta baseada em Java, portátil e prática para análise de regressão. Ele oferece simplicidade e flexibilidade para usuários que precisam de uma solução leve e acessível.

Características principais:

• Funciona em Windows, Linux e Mac;
• Requer Java instalado para ser executado;
• Permite realizar análises estatísticas rapidamente, mesmo em computadores mais modestos.

Ponto forte:

Por ser portátil, o Statcato não exige instalação completa, tornando-o ideal para usuários que precisam de um software funcional em diferentes dispositivos.

4. Jamovi

O Jamovi combina um design moderno com funcionalidades poderosas para análise de regressão e outros métodos estatísticos. Ele é projetado para ser uma solução acessível e fácil de usar, mesmo para quem não tem muita experiência com estatística.

Características principais:

• Compatível com Windows, Linux, Mac e Chrome OS;
• Interface limpa e intuitiva, ideal para estudantes e profissionais;
• Suporte para múltiplas técnicas de análise de dados, além de regressão.

Por que escolher o Jamovi?

Se você está buscando um software que ofereça uma experiência fluida e agradável, o Jamovi é uma excelente escolha. Sua interface moderna facilita a exploração de dados e a geração de relatórios.

Aplicações práticas da regressão linear

A regressão linear é uma ferramenta que encontra aplicações em diversas áreas, graças à sua simplicidade e eficácia para analisar relações entre variáveis. Vamos explorar algumas das principais formas como ela é usada no dia a dia.

1. Previsão de vendas

Uma das aplicações mais comuns da regressão linear é na previsão de vendas. As empresas utilizam dados históricos para identificar padrões e tendências, permitindo prever resultados futuros.

Como funciona na prática?

Por exemplo, uma loja pode usar a regressão linear para correlacionar seus gastos com publicidade ao volume de vendas. Se os dados mostrarem que cada R$ 1.000,00 investido em anúncios gera um aumento de 5% nas vendas, a empresa pode ajustar seu orçamento publicitário para maximizar os lucros.

Benefícios:

• Planejamento estratégico mais eficiente;
• Previsão mais precisa de demandas, ajudando na gestão de estoques;
• Suporte na definição de campanhas de marketing direcionadas.

2. Análise de tendências

A regressão linear é muito usada para identificar tendências em séries temporais, como mudanças ao longo do tempo em vendas, preços, ou comportamentos de consumo.

Exemplo prático:

Um analista pode estudar as vendas anuais de um produto nos últimos cinco anos e perceber que elas aumentam em média 10% ao ano. Com base nessa análise, ele pode projetar o desempenho esperado para os anos seguintes e ajudar a empresa a se preparar para atender à demanda futura.

Outros casos de uso:

• Análise de crescimento populacional em uma região;
• Monitoramento de preços em um mercado competitivo;
• Identificação de sazonalidade em vendas (como o aumento de compras no final do ano).

3. Exemplos em diferentes setores

A versatilidade da regressão linear permite sua aplicação em diversos campos, cada um com seus próprios desafios e oportunidades.

Negócios:

No setor corporativo, é comum usar a regressão linear para entender como diferentes fatores influenciam os resultados financeiros.

• Exemplo: determinar a relação entre gastos com marketing digital e aumento no número de clientes adquiridos.

Medicina:

Na área da saúde, a regressão linear auxilia no estudo de relações entre variáveis médicas.

• Exemplo: avaliar como diferentes dosagens de um medicamento afetam a pressão arterial dos pacientes, ajudando a determinar a dose mais eficaz.

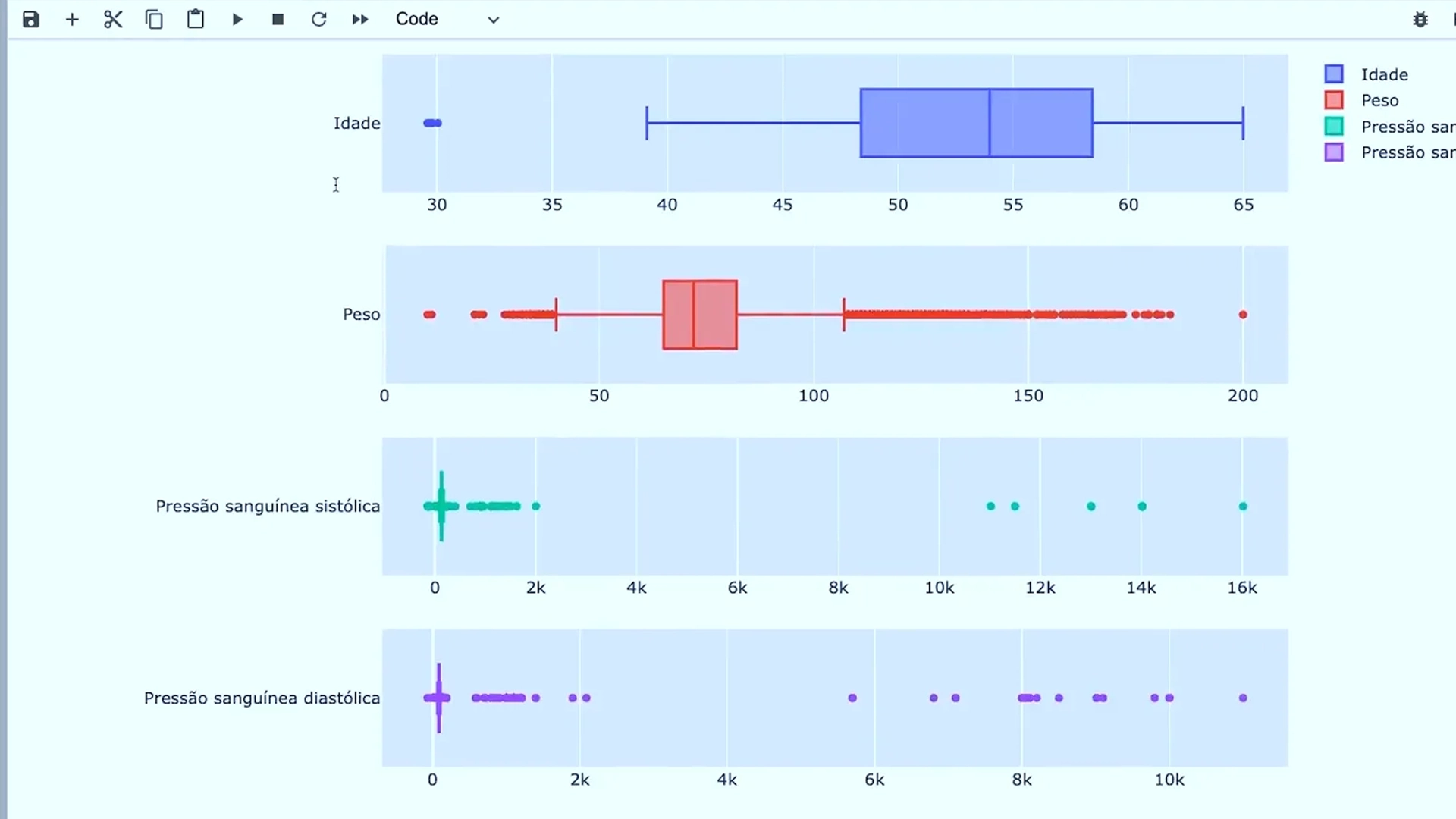
Prevendo risco de doenças cardíacas com Machine Learning

Implementando regressão linear em Python

Agora que já exploramos os conceitos básicos da regressão linear e suas aplicações, é hora de aprender como implementá-la utilizando Python. A linguagem oferece diversas bibliotecas que facilitam a criação e a análise de modelos de regressão linear.

Bibliotecas recomendadas

Para trabalhar com regressão linear em Python, as duas bibliotecas mais utilizadas são:

1. Scikit-learn
   • Uma das bibliotecas mais poderosas para aprendizado de máquina;
   • Inclui ferramentas práticas para criar e avaliar modelos de regressão linear.
2. Statsmodels
   • Focada em análises estatísticas e econométricas.
   • Permite estimar modelos estatísticos e fornece relatórios detalhados sobre os resultados.

Passo a passo para criar um modelo de regressão linear em Python

Vamos detalhar cada etapa para criar um modelo funcional:

1. Importar as bibliotecas necessárias

import pandas as pd  
import numpy as np  
from sklearn.model_selection import train_test_split  
from sklearn.linear_model import LinearRegression  
import matplotlib.pyplot as plt  

2. Carregar os dados

Carregue o arquivo contendo os dados que serão analisados.

data = pd.read_csv('seus_dados.csv')  

3. Preparar os dados

Escolha a variável independente (X) e a variável dependente (y).

X = data[['variavel_independente']]  
y = data['variavel_dependente']  

4. Dividir os dados em conjuntos de treino e teste

A divisão dos dados é importante para treinar o modelo e avaliá-lo com um conjunto de dados não utilizado no treino.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  

5. Criar o modelo de regressão linear

Utilize a biblioteca Scikit-learn para instanciar e ajustar o modelo.

model = LinearRegression()  
model.fit(X_train, y_train)  

6. Fazer previsões

Use o modelo treinado para prever valores no conjunto de teste.

predictions = model.predict(X_test)  

Exemplo prático: prevendo vendas com base em gastos publicitários

Abaixo está um exemplo completo para prever vendas com base nos gastos com publicidade:

import pandas as pd  
from sklearn.model_selection import train_test_split  
from sklearn.linear_model import LinearRegression  
import matplotlib.pyplot as plt  

# Carregar os dados  
data = pd.read_csv('seus_dados.csv')  

# Preparar os dados  
X = data[['gastos_publicidade']]  
y = data['vendas']  

# Dividir os dados  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  

# Criar o modelo  
model = LinearRegression()  
model.fit(X_train, y_train)  

# Fazer previsões  
predictions = model.predict(X_test)  

# Visualizar os resultados  
plt.scatter(X_test, y_test, color='blue', label='Dados reais')  
plt.plot(X_test, predictions, color='red', label='Previsões')  
plt.xlabel('Gastos com Publicidade')  
plt.ylabel('Vendas')  
plt.title('Regressão Linear - Gastos x Vendas')  
plt.legend()  
plt.show()  

Explicação do código:

1. Carregar e preparar os dados:
   • Carrega o conjunto de dados usando pandas;
   • Define as variáveis independente (gastos) e dependente (vendas).
2. Divisão de dados:
   • Divide os dados em 80% para treino e 20% para teste usando train_test_split.
3. Treinamento do modelo:
   • Treina o modelo com os dados de treino usando LinearRegression().fit().
4. Predição e visualização:
   • Realiza previsões no conjunto de teste e cria um gráfico para comparar os valores reais com os previstos.

Benefícios da visualização dos resultados

O gráfico gerado ajuda a interpretar os resultados da regressão. Pontos azuis representam os dados reais, enquanto a linha vermelha mostra o modelo ajustado. Quanto mais próximos os pontos estiverem da linha, melhor será o desempenho do modelo.

Com esse passo a passo, você pode implementar modelos de regressão linear para explorar e analisar seus próprios conjuntos de dados!

Dê o próximo passo na sua carreira

Neste guia, você aprendeu os fundamentos da regressão linear, incluindo suas bases matemáticas, tipos, aplicações práticas e como implementá-la em Python. Essa técnica é uma das mais poderosas em ciência de dados, permitindo analisar informações complexas, extrair insights valiosos e tomar decisões embasadas.

Se você deseja ir além e aprofundar seus conhecimentos em machine learning e ciência de dados, a Trilha Data Science & Machine Learning, da Asimov Academy é o próximo passo ideal. Nessa trilha, você aprenderá desde os fundamentos da área até técnicas avançadas de análise e modelagem de dados, com aplicações práticas que ajudam a consolidar o aprendizado.

Com uma abordagem clara e prática, você desenvolverá habilidades essenciais, como:

• Manipular e tratar grandes volumes de dados;
• Aplicar estatística e matemática de forma eficiente;
• Criar modelos robustos de machine learning, como regressão e classificação.

Não importa se você está começando do zero ou já tem alguma experiência, essa trilha foi projetada para preparar você para os desafios do mercado.

Clique logo abaixo para conhecer a Trilha Data Science & Machine Learning  e transforme seu conhecimento em uma carreira de sucesso.

Data Science & Machine Learning