Elbow Method e Silhouette Score: como identificar o número ideal de clusters

Em um mundo impulsionado por dados, encontrar sentido no caos é essencial para tomadas de decisão inteligentes e estratégicas. É aqui que o clustering entra em cena. Imagine poder organizar grandes volumes de informação em grupos coerentes, revelando padrões e insights ocultos. Essa é a proposta dessa técnica de aprendizado de máquina, que transforma dados brutos em conhecimento valioso.

Antes de falarmos sobre Elbow Method e Silhouette Score, é importante entender o conceito de clusters. Um cluster é um grupo de dados que compartilham características semelhantes, organizados com base em critérios ou métricas específicas.

O que é Clustering?

No contexto de machine learning, o clustering é uma técnica de aprendizado não supervisionado usada para identificar padrões e estruturas ocultas nos dados. Alguns dos algoritmos mais conhecidos para realizar clustering incluem K-Means, DBSCAN e Hierarchical Clustering, cada um com abordagens distintas para agrupar os dados.

Além de ser uma técnica poderosa para simplificar a complexidade dos dados, a clusterização resolve diversos problemas de negócios.

Principais aplicações

1. Segmentação de clientes, ajudando a personalizar estratégias de marketing;
2. Detecção de anomalias, identificando fraudes ou eventos fora do padrão;
3. Planejamento de localização, escolhendo pontos estratégicos para novos negócios;
4. Gestão de produtos e estoque, otimizando o portfólio e a previsão de demanda;
5. Melhoria na experiência do usuário, personalizando interações e recomendações.

Em resumo, os clusters são ferramentas fundamentais para extrair valor dos dados e apoiar decisões estratégicas em diferentes áreas.

Método Elbow

O Método Elbow é uma abordagem visual para encontrar k, baseada na análise do within-cluster sum of squares (WCSS), que mede a variação dentro dos clusters. A ideia é identificar o “cotovelo” no gráfico, onde a taxa de diminuição muda para cada k significativamente.

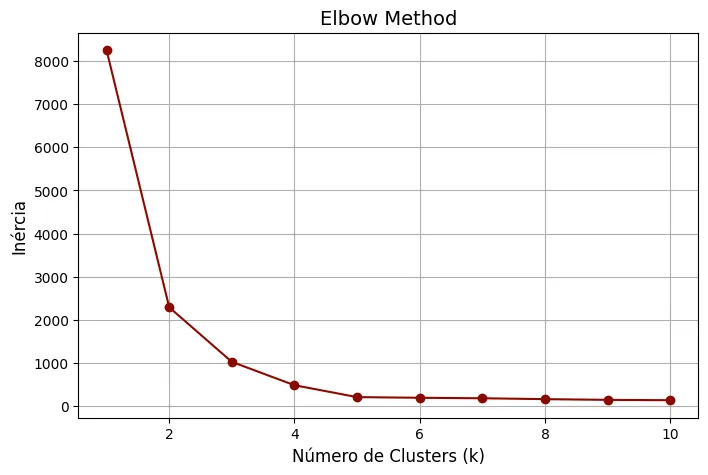
Exemplo em Python:

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# Gerando dados simulados
X, _ = make_blobs(n_samples=300, centers=5, cluster_std=0.6, random_state=0)

# Calculando a inércia para diferentes valores de k
inertia = []
k_values = range(1, 11)
for k in k_values:
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(X)
inertia.append(kmeans.inertia_)

# Plotando o Elbow Method
plt.figure(figsize=(8, 5))
plt.plot(k_values, inertia, '-o', color='#8d0801')
plt.title('Elbow Method', fontsize=14)
plt.xlabel('Número de Clusters (k)', fontsize=12)
plt.ylabel('Inércia', fontsize=12)
plt.grid()
plt.show()

Silhouette Score

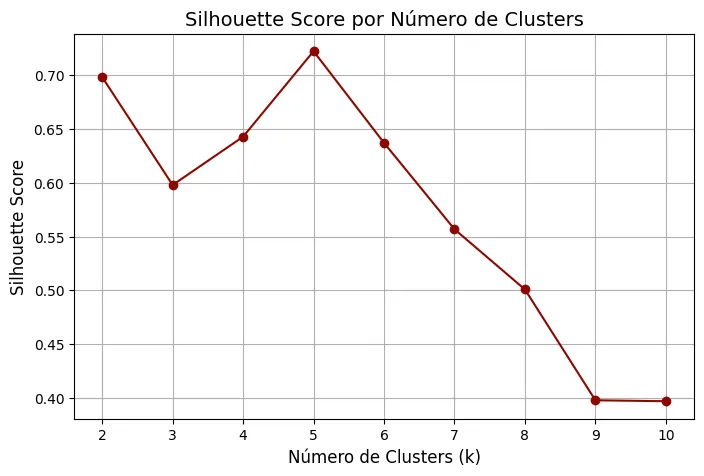
O Silhouette Score mede a semelhança de um ponto de dados dentro de seu cluster (coesão) em comparação com outros clusters (separação).

S(i) = b(i) – a(i) / max {a(i),b(i)}

1. S(i) é o coeficiente de silhueta do ponto i;
2. a(i) é a distancia média entre “i” e todos os outros pontos de dados no cluster ao qual ele pertence;
3. b(i) é a distancia média de “i” a todos os clusters que ele não pertence.

Exemplo em Python:

from sklearn.metrics import silhouette_score

# Calculando o Silhouette Score para diferentes valores de k
silhouette_scores = []
for k in range(2, 11):
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(X)
score = silhouette_score(X, kmeans.labels_)
silhouette_scores.append(score)

# Plotando o Silhouette Score
plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_scores, '-o', color='#8d0801')
plt.title('Silhouette Score por Número de Clusters', fontsize=14)
plt.xlabel('Número de Clusters (k)', fontsize=12)
plt.ylabel('Silhouette Score', fontsize=12)
plt.grid()
plt.show()

O valor do coeficiente de Silhueta estará entre [-1,1], uma pontuação de 1 denota o melhor resultado significando que o ponto de dados “i” é muito compacto dentro de seu cluster e distante de outros clusters, com -1 sendo o pior resultado possível e 0 representando dados aglomerados e sobrepostos.

Conclusão

O Método Elbow e o Silhouette Score são ferramentas indispensáveis para a determinação do número ideal de clustering em análises de agrupamento. O Método Elbow, por meio de uma abordagem visual, facilita a identificação do ponto em que adicionar mais clusters deixa de trazer benefícios significativos, mas, por outro lado, o Silhouette Score complementa essa análise ao avaliar a qualidade dos clusters formados, considerando tanto a coesão interna quanto a separação entre grupos distintos. Ao utilizar essas duas técnicas em conjunto, analistas de dados conseguem tomar decisões mais embasadas, garantindo resultados mais precisos e representativos. 

Se você deseja aprofundar ainda mais seus conhecimentos e se tornar um cientista de dados, conheça a nossa Trilha Data Science & Machine Learning. Inicie sua carreira na área mais aquecida do mercado! A Trilha é ideal para quem deseja começar do zero com cursos introdutórios e avançar até os módulos de machine learning, adquirindo também conhecimentos essenciais em matemática e estatística. Tudo isso com a didática clara e concisa da Asimov, uma escola especializada em Python e educação para cientistas de dados.

Na Trilha Data Science & Machine Learning, você aprenderá a armazenar, tratar e apresentar grandes conjuntos de dados, dominar conceitos fundamentais de estatística e aplicar técnicas avançadas para criar modelos robustos e poderosos. Não perca a chance de transformar sua carreira!

Trilha Data Science e Machine Learning